Discrete-time Signal Processing (2)
Definition of z-transform and Fourier Transform
Fourier Transform :
\[X(e^{j\omega}) = \displaystyle{ \sum_{n=-\infty}^{\infty}x[n]e^{-j\omega n} }\]
Z-Transform :
\[X(z) = \displaystyle{ \sum_{n=-\infty}^{\infty}x[n]z^{-n} }\]
\[X(z) = \displaystyle{ \sum_{n=-\infty}^{\infty}x[n]r^{-n}e^{-j\omega n} }\]
When r=1 then it contain Fourier transform
For the z-transform to be meaningful, then the function obtained by the transformation must converge at a finite point, i.e
\[|X(z)| <\infty\]
 ## The Inverse Z-transform
## The Inverse Z-transform
\[x[n] = \displaystyle{\frac{1}{2\pi j}}\oint_{C}X(z)z^{n-1}dz\]
Partial Fraction Expansion Method
\[\displaystyle{X(z) = \frac{b_0}{a_0}\frac{\prod_{k=1}^{M}(1-c_kz^{-1})}{\prod_{k=1}^{N}(1-d_kz^{-1})}}\]
If M < N \[X(z) = \displaystyle{\sum_{k=1}^{N}\frac{A_k}{1-d_kz^{-1}}}\]
\[(1-d_kz^{-1})X(z)|_{z=d_k} = A_k\]
IF M > N
\[X(z) = \displaystyle{ \sum_{r=0}^{M-N}B_rz^{-r} +\sum_{k=1}^{N}\frac{A_k}{1-d_kz^{-1}}}\]
If M≥N and X(z) has higher order s, poles at z=di \[X(z) = \displaystyle{ \sum_{r=0}^{M-N}B_rz^{-r} +\sum_{k=1,k\neq i}^{N}\frac{A_k}{1-d_kz^{-1}}+\sum_{m=1}^s\frac{C_m}{(1-d_iz^{-1})^m}}\]
\[\displaystyle{C_m = \frac{1}{(s-m)!(-d_i)^{s-m}}}\left\{ \frac{d^{s-m}}{d\omega^{s-m}}[(1-d_i\omega)^sX(\omega^{-1})]\right \}_{\omega=d_i^{-1}}\]
porpertys of z-transform
PROPERTY 1:
The ROC is a ring or disk in the z-plane centered at the origin; i.e.,
\[0<= r_R< |z|< r_L <=\infin\]
PROPERTY 2:
The Fourier transform of x[n] converges absolutely if and only if the ROC of the z-transform of x[n] includes the unit circle.
PROPERTY 3:
The ROC cannot contain any poles.
PROPERTY 4:
If x[n] is a finite-duration sequence, i.e., a sequence that is zero except in a finite interval -∞ < N1≤n≤ N2< ∞, then the ROC is the entire z-plane, except possibly z =0 or z = ∞.
PROPERTY 5:
If x[n] is aright-sided sequence, i.e., a sequence that is zero for n < N1 < ∞, the ROC extends outward from the outermost (i.e., largest magnitude) finite pole in X(z) to (and possibly including) z = ∞. It can be causal
PROPERTY 6:
If x[n] is a left-sided sequence, i.e., a sequence that is zero for n >N2> -∞, the ROC extends inward from the innermost (smallest magnitude) nonzero pole in X(z) to (and possibly including) z = 0. It cannot be causal
PROPER TY 7:
A two-sided sequence is an infinite-duration sequence that is neither right sided nor left sided. If x[n] is a two-sided sequence, the ROC will consist of a ring in the z-plane, bounded on the interior and exterior by a pole and, consistent with property 3, not containing any poles. It is stable
PROPERTY 8:
The ROC must be a connected region.
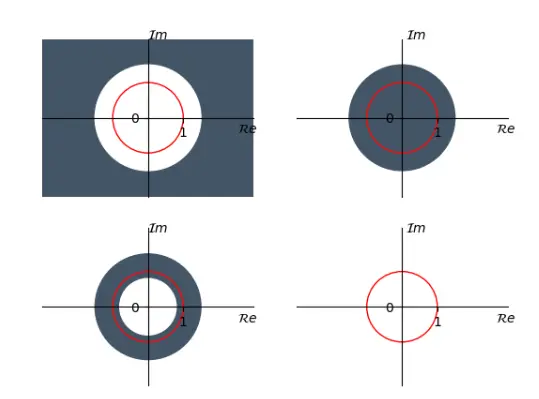
The shaded part of the graph is the convergence domain, where the red circle is |z|=r=1, that is, the Fourier transform, and if the convergence domain of the z-transform contains r=1 a circle of , it indicates the convergence of the Fourier transform of the sequence.



