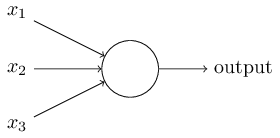
Evolutionary Algorithms
What is an Evolutionary Algorithm?
It is a type of optimization algorithm inspired by the principles of natural selection and genetics. It's used to solve complex problems by evolving potential solutions over time, mimicking the process of biological evolution.
Main EA components:
- Representation: encoding of solutions
- Evaluation: fitness function
- Population: set of candidate solutions
- Selection: method to choose parents
- Survivor selection: method to choose individuals for the next generation
- Recombination: method to combine parents to create offspring
- Mutation: method to introduce random changes to offspring
Scheme of Evolutionary Algorithms
1 | BEGIN |
Main EA components:
Representation
Role: provides code for candidate solutions that can be manipulated by variation operators
It incloud two types:
- Phenotype: object in orginal problem space
- genotype: code to denote that object, the inside (chromosome, “digital DNA”)
Implies two mappings:
Encoding : phenotype=> genotype (not necessarily one to one)
Decoding : genotype=> phenotype (must be one to one)
Examples:
Binary representation
- Genotype: 01001011
- Phenotype: 83
Real-valued representation
- Genotype: [0.1, 0.2, 0.3, 0.4]
- Phenotype: (0.1, 0.2, 0.3, 0.4)
Permutation representation
- Genotype: [3, 1, 2, 4]
- Phenotype: (1, 2, 3, 4)
The order is important, different order means different solution.
Evaluation
Role: provides fitness values for candidate solutions
Fitness function: function that maps candidate solutions to fitness values
Fitness value: measure of quality of a candidate solution
Fitness landscape: graph of fitness values for all candidate solutions
Population
Role: holds the candidate solutions of the problem as individuals (genotypes)
Population size: number of candidate solutions in a population
Selection operators act on population level
Variation operators act on individual level
Diversity
Diversity of a population refers to the number of different fitnesses / phenotypes / genotypes present (note: not the same thing)
Selection pressure
Takeover time \(\tau^*\) is a measure to quantify the selection pressure
\[\tau^* = \frac{\ln(\lambda)}{\ln(\frac{\lambda}{\mu})}\]
where $\lambda$ is the number of offspring produced per generation and $\mu$ is the population size.Relationship:
High selection pressure -> Low diversity
Low selection pressure -> High diversitySelection
Role: Identifies individuals to become parents or to survive
Usually probabilistic
high quality solutions more likely to be selected than low quality
even worst in current population usually has non-zero probability of being selected
When do this

Selection methods:
Roulette wheel selection
- Parents are chosen based on their fitness values
- Better solutions have a higher chance of being selected
Tournament selection
- Parents are chosen based on a random sample of the population
- The best solution in the sample is selected
Rank-based selection
Variation
Role: Generates new candidate solutions from parents
Usually divided into two types according to their arity (number of inputs):
- Arity 1 : mutation operators
- Arity >1 : recombination operators
- Arity = 2 typically called crossover
- Arity > 2 is formally possible, seldom used in EC
Variation operators:
Crossover
- Combines two parents to create offspring
- Commonly used in genetic algorithms
- Can be used to introduce new genetic material into the population
Order 1 crossover

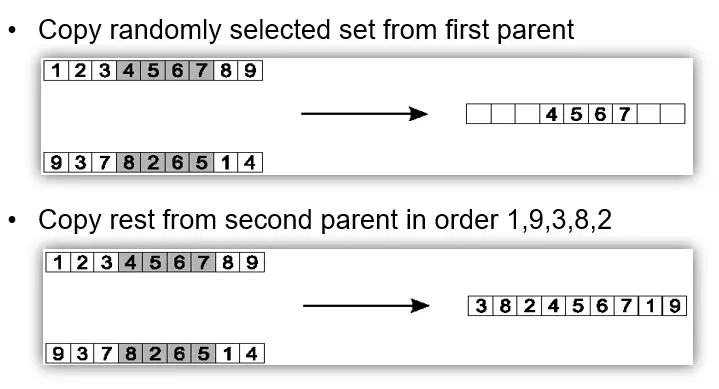
Partially Mapped Crossover (PMX)

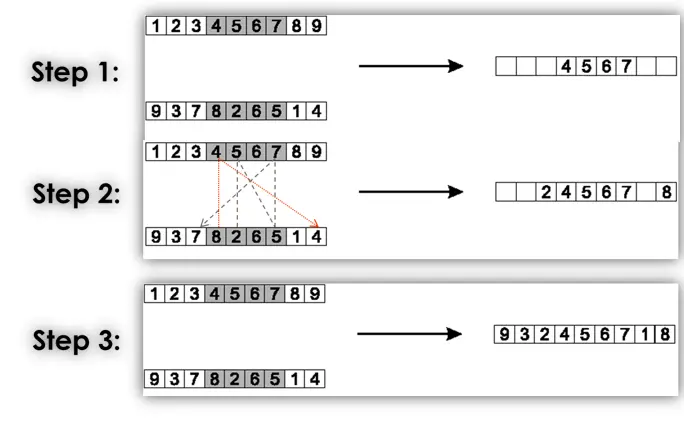
Cycle crossover (CX)


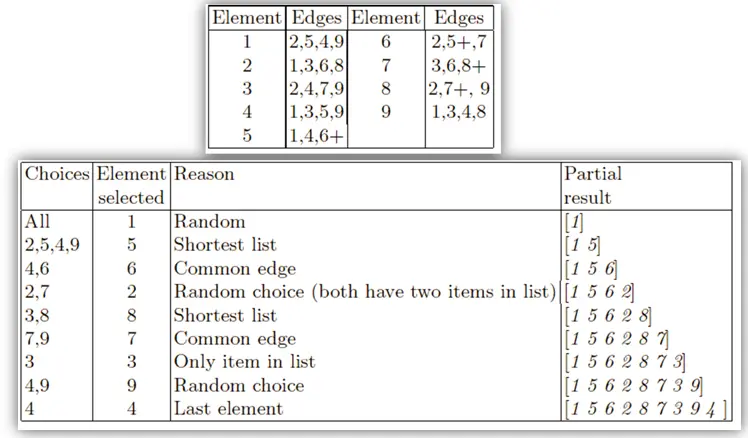
Edge recombination

one-point crossover
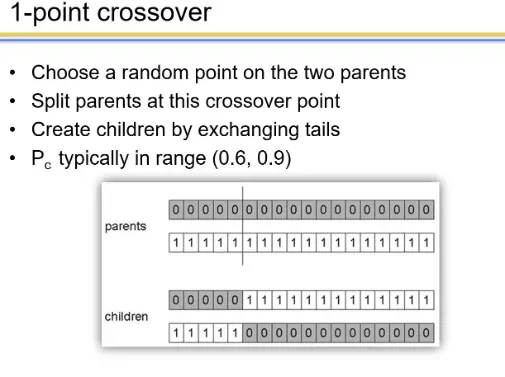
- More likely to keep together genes that are near each other
- Can never keep together genes from opposite ends of string
- This is known as Positional Bias
- Can be exploited if we know about the structure of our problem, but this is not usually the case
n-point crossover
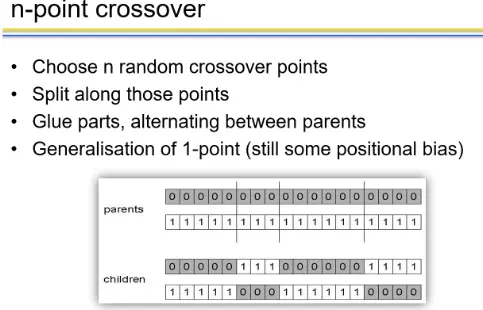
n-point crossover has an inherent bias in that it tends to keep together genes that are located close to each other
Uniform crossover

In contrast, uniform crossover does not exhibit any positional bias. However, unlike n-point crossover, uniform crossover does have a strong tendency towards transmitting 50% of the genes from each parent and against transmitting an offspring a large number of coadapted genes from one parent. This is known as distributional bias.
Mutation
- Introduces random changes to an individual
Unifor mutation

Non-uniform mutation

adaptive mutation:
The essential feature is that the step sizes are also included in the chromosomes and they themselves undergo variation and selection.
Mutation step size is not set by user but coevolves with solution