A Low-Complexity Modified ThiNet Algorithm for Pruning Convolutional Neural Networks

Introduction

In this artical, scholars proposed a faster version of the ThiNet algorithm(F-ThiNet). They want to remove all the filters from the network and can be selected in a single step rather than selecting the filters one by one iteratively.

F-ThiNet

In the ThiNet method, K filters from a total of \(H_l\) filters of the \(l^{th}\) convolutional layer are removed so that their removal has the minimum effect on an aggregate value of a combination of the values of some selected entries in the out put of the \((l+1)^{st}\) convolutional layer, using m input images.ThiNet use the equations below to choose the filters. \[ A_{T}=\sum_{i=1}^{m}\left(\sum_{j \in T} \hat{X}_{i, j}^{l+1}\left[p_{1}, p_{2}, p_{3}\right]\right)^{2} (1) \] \[ argmin\{A_T\} (2) \] \(\hat{X}_{i, j}^{l+1}\left[p_{1}, p_{2}, p_{3}\right]\) is the value of the entry of the output of the \((l+1)^{st}\) convolutional layer generated by the \(i^{th}\) input image and filter j in the subset T of indices of the filters in the \(l^{th}\) convolutional layer.

In F-Thinet, in each iteration, the index of on additional filter from the \(l^{th}\) convolutional layer is added to it.(意思是每次迭代会选一个卷积层中的一个卷积核剔除掉) In the beginning of the \(r^{th}\) iteration, the set T has indices of r-1 that were selected from the \(l^{th}\) convolutional layer in the previous iterations.(第r次迭代以后，就已经选取了r-1个需要剔除的卷积核). During the \(r^{th}\) iteration, the size of the set T is increased by unity by adding to it the index of that filter from the remaining filters of the \(l^{th}\) convolutional layer that uses (1) and (2).(在第r次迭代中，通过thinet的公式进行选取需要剔除的卷积核)When the filter in the \(r^{th}\) iteration is selected, the argmin(求该函数有最小结果时候的取值) in ThiNet(2) operates on \(H_l\) values computed in ThiNet(1). For each of these \(H_l\) values, the number of multiplications per image needed is given by \[ N_{l, r, I}=\left[\left(\sum_{i=1}^{l-1} C_{i, H_{i}}\right)+C_{l, r}+r I k_{l+1}^{2}\right] \]

\(C_{\mu, \nu}=\nu k_{\mu}^{2} H_{\mu-1} L_{\mu} W_{\mu}\left(\mu=1, \ldots, \Omega ; \nu=1, \ldots, H_{\mu}\right)\) and I is the number of selected entries in the output of the \((l+1)^{st}\) convolutional layer.(这两个变量是代表第l+1层卷积层的输出中所选出来的数据)The three terms in this equation compute, respectively, the number of multiplications in the convolutional layers preceding the pruned layer l, the number of the multiplications in the \(l^{th}\) layer when it contains r filters, and the number of multiplications in the \((l+1)^{st}\) convolutional layer when each filter has r channels.(公式中的3个部分分别代表了修剪卷积层l前相乘的数量，第l层包含r个过滤器（卷积核）是进行相乘的数量以及在（l+1)卷积层中每个filter包含r个通道时相乘的数量。）

伪代码如下：

In ThiNet,to select K filters from the \(l^{th}\) convolutional layer needs \(\sum_{i=1}^{K}\left(H_{l}-i+1\right) N_{l, i, I}\) multiplications. But in F-ThiNet they only need \(H_lN_{l,1,I}\) which is independent of K. Therefore, the computations needed to select K filters in the \(l^{th}\) convolutional layer in the F-ThiNet algorithm is the same as the amount of computations needed for the selection of the first filter in the ThiNet algorithm, thus making the proposed F-Thinet algorithm to have a significantly reduced complexity.

Experiments

The ThiNet and F-ThiNet are individually emmployed by scholars for pruning two different networks, VGG-16 and AlexNet, on two datasets, CIFAR-10 and Fashino-MNIST.

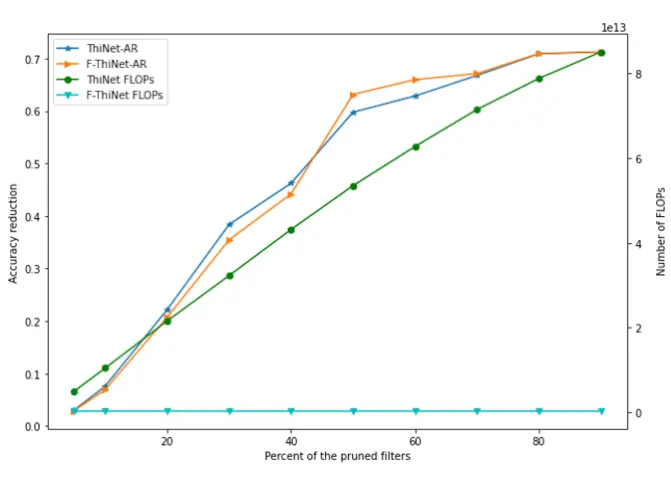
This picture shows the accuracy reduction (AR) of VGG-16 with CIFAR-10 dataset images as its input, when the same % of filters from all its convolutional layers is pruned using ThiNet and F-ThiNet vs number of FLOPs required.(FLOPs means 每秒浮点计算数)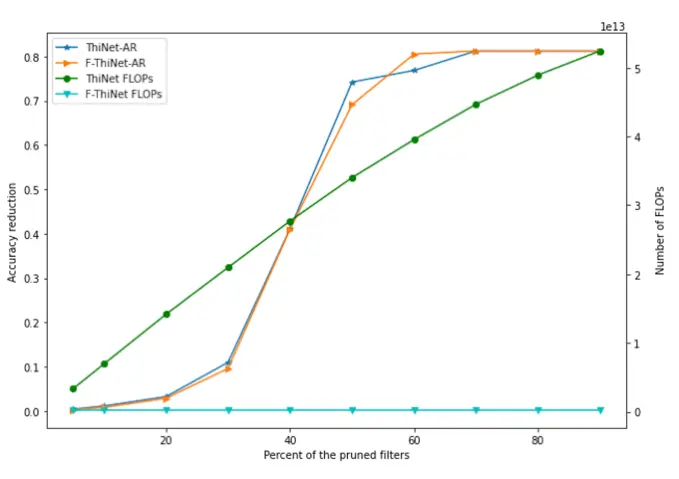

This picture shows the accuracy reduction (AR) of VGG-16 with Fashion-MNIST dataset images as its input, when the same % of filters from all its convolutional layers is pruned using ThiNet and F-ThiNet vs number of FLOPs required.

It is seen from this figure that generally there is no significant difference in the accuracy reduction of the pruned networks resulting from the two algorithms, irrespective of the percentage of filters removed. On the other hand, the proposed F-ThiNet algorithm requires much less number of FLOPs for pruning the network.

Conclusion

There is a very significant difference in the number of FLOPs required by the two pruning methods in that the number FLOPs required by F-ThiNet is less than 2% of that required by ThiNet.But the accuracy between these two algorithm is about the same. So the major advantage of the proposed algorithm is that its time-complexity is significantly lower than that of ThiNet or any other state-of-the art algorithm.