Mathematical Statements

Atomic Statements and Molecular Statements

如果一个句子不能被分割成更小的声明，那就是atmoic的否则就是molecular的。
Example：
atomic的
1. Telephone numbers in the USA have 10 digits.
2. The moon is made of chees.
3. 42 is a perfect square.
4. Every even number greather than 2 can be expressed as the sum of two primes.
molecular的
Telephone numbers in the USA have 10 digits and 42 is a perfect square. ### Logical Connectives:

symbol read meaning
∧ and conjunction
∨ or disjunction
→ if..then implication or conditional
↔︎ if and only if biconditional
¬ not negation

Notice

  • 在implication的语句中，只有if部分是真then部分是假时整个statement 才是 false的
  • Converse是指P→Q 和 Q→P的关系， 一个implication的converse是否为真与original implication 无关。
  • Contrapositive指的是 P→Q 和 ¬Q→¬P的关系。 一个implication的contraspositive和original implication的逻辑是相同的，要么both为真要不both为假

Sets(集合)

Set 就是一个无序(unordered)的对象集合。 Example: \[A=\{1,2,3\}\] 读作“A is the set containing the elements 1,2 and 3"使用大括号(curly braces)去enclose 这些 element。
\[a \in \{a,b,c\}\] The symbol \(\in\) is read “is in” or “is an element of.” 意思是a是这个集合中的一个元素（element）。
Special symbol

Symbol Meaning
\(\emptyset\) The empty set is the set which contains no elements.
\(\mathcal{U}\) The universe set is the sest of all elements.
\(\mathbb{N}\) The set of natural numbers. That is, \(\mathcal{N}=\{0,1,2,3...\}\)
\(\mathbb{Z}\) The set of integers. That is, \(\mathcal{Z}=\{...-3,-2,-1,0,1,2,3...\}\)
\(\mathbb{Q}\) The set of rational numbers.
\(\mathbb{R}\) The set of real numbers.
\(\mathcal{p}(A)\) The poser set of any set A is the set of all subsets of A

Function(函数)

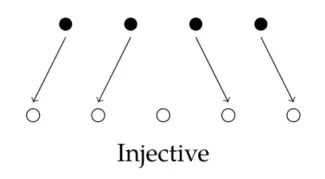
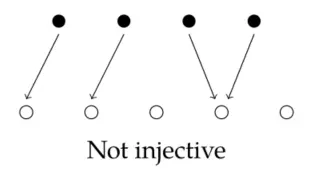
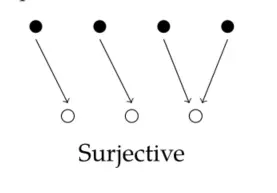
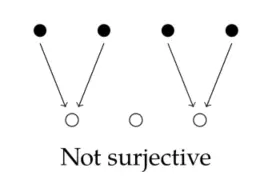
image
image
image
image