堆排序
概念
堆排序是利用 堆进行排序的 堆是一种完全二叉树 堆有两种类型: 大根堆 小根堆 两种类型的概念如下: 大根堆:每个结点的值都大于或等于左右孩子结点 小根堆:每个结点的值都小于或等于左右孩子结点
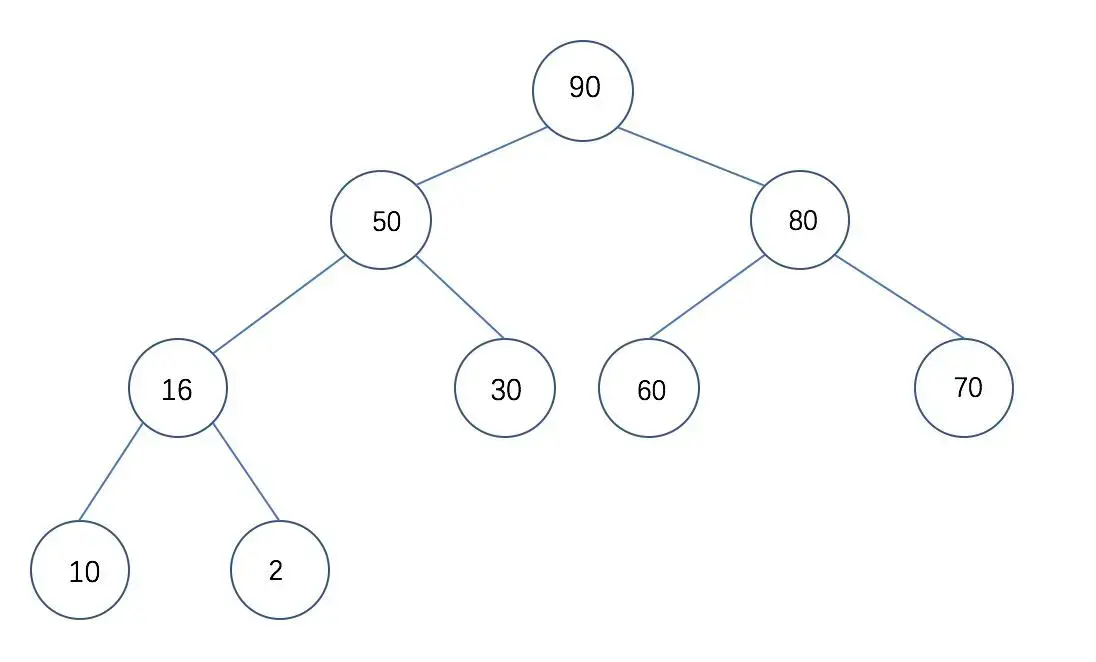
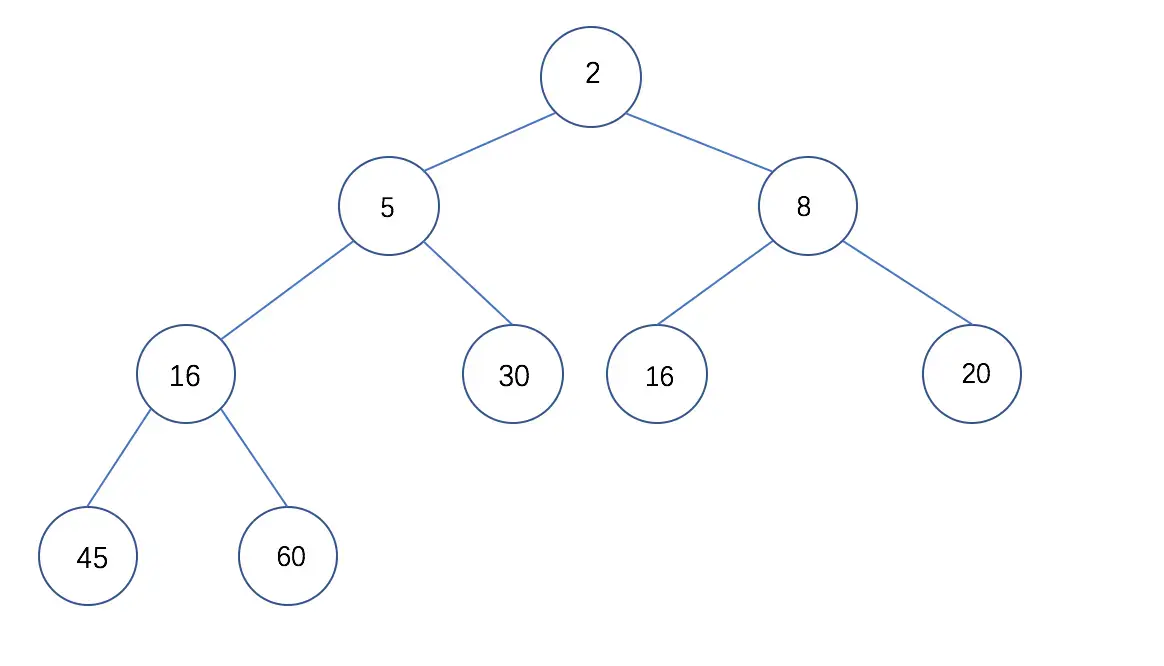
算法过程
如何把一个序列构造出一个大根堆 输出堆顶元素后,如何使剩下的元素构造出一个大根堆

python实现如下 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25def build_heap(arr,star,end): #用于构建大根堆
temp=arr[star]
i=star
j=2*i #左子节点的索引为2*i 右子节点为2*i+1
while j<=end:
if j<end and arr[j]<arr[j+1]: #比较左右子节点大小,选取大的作为用于替换的节点
j+=1
if temp<arr[j]: #判断子节点是否比父节点大,是则互换
arr[i]=arr[j]
i=j #互换以后将比较节点移动到子节点上
j=2*i #在下一循环中比较子节点和子节点的子节点
else:
break
arr[i]=temp
def swap(arr,i,j):
arr[i],arr[j]=arr[j],arr[i]
def heap_sort(arr):
L_length=len(arr)-1
first_count=L_length//2 #最后一个父节点的索引
for i in range(first_count):
build_heap(arr,first_count-i,L_length) #构建第一个大根堆
for i in range(L_length-1):
swap(arr,1,L_length-i) #替换第一个节点和最后一个未排序的节点
build_heap(arr,1,L_length-i-1)#对剔除最后一个节点的堆重新构造大根堆
return [arr[i] for i in range(1,len(arr))]



